Wheel factorization

Wheel factorization is a graphical method for manually performing a preliminary to the Sieve of Eratosthenes that separates prime numbers from composites. Start by writing the natural numbers around circles as shown below. Prime numbers in the innermost circle have their multiples in similar positions as themselves in the other circles, forming spokes of primes and their multiples. Multiples of the prime numbers in the innermost circle form spokes of composite numbers in the outer circles.

Contents

Procedure

  1. Find the first few prime numbers. They are known or can be found quickly using Sieve of Eratosthenes.
  2. Multiply the prime numbers together to give the result n.
  3. Write 1 to n in a circle. This will be the inner-most circle.
  4. Taking x to be the number of circles written so far, continue to write xn + 1 to xn + n in another circle around the inner-most circle, such that xn + 1 is in the same position as (x − 1)n + 1.
  5. Repeat step 4 until the largest number to be tested for primality.
  6. Strike off the number 1.
  7. Strike off the spokes of prime numbers (found in step 1) with its multiples without striking off the numbers in the inner-most circles.
  8. Strike off the spokes of all multiples of prime numbers found in step 1.
  9. The remaining numbers in the wheel contain mostly prime numbers. Use other methods such as Sieve of Eratosthenes to remove the remaining non-primes.

Example

1. Find the first 2 prime numbers—2 and 3.

2. n = 2 · 3 = 6

3.

 1  2  3  4  5  6

4. x = 1. xn + 1 = 1 · 6 + 1 = 7. (x + 1)n = (1 + 1) · 6 = 12. Write 7 to 12 with 7 aligned with 1.

 1  2  3  4  5  6
 7  8  9 10 11 12

5. x = 2. xn + 1 = 2 · 6 + 1 = 13. (x + 1)n = (2 + 1) · 6 = 18. Write 13 to 18. Repeat for the next few lines.

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

6 and 7. Sieving

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

8. Sieving

 1  2  3  4  5  6
 7  8  9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

9. Resultant list contains a non-prime 25. Use other methods of sieve to arrive at

2 3 5 7 11 13 17 19 23 29

Analysis and Computer implementation

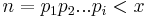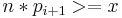Given a number k > n, we know that it is not prime if k mod n and n are not relatively prime. The fraction of numbers that the wheel sieve eliminates is 1 - phi (n) / n, which is also the efficiency of the sieve. From the properties of phi, it can easily be seen that the most efficient sieve smaller than x is the one where n = p_1 p_2 ... p_i < x and n * p_{i%2B1} >= x . It can also be demonstrated that this efficiency rises very slowly for large n.

To be of maximum use on a computer, we want the numbers that are smaller than n and relatively prime to it as a set. Using a few observations, the set can easily be generated :

  1. Start with 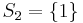S_2 = \{1\} , which is the set for n=2 .
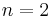  2. Let 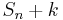S_n %2B k be the set where k has been added to each element of S_n .
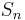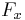  3. Then S_{n p_{i%2B1}} = F_{p_{i%2B1}} [S_n \cup S_n %2B n \cup S_n %2B 2n \cup ... \cup S_n %2B n (p_{i%2B1} - 1)] where F_x represents the operation of removing all multiples of x.
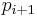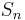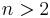  4. 1 and p_{i%2B1} will be the two smallest of S_n when n > 2 removing the need to compute prime numbers separately
  5. The set is symmetrical around 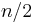n / 2 , reducing storage requirements.

External links

Primality tests
Sieving algorithms
Integer factorization algorithms
Multiplication algorithms
Discrete logarithm algorithms
GCD algorithms
Modular square root algorithms
Other algorithms
Italics indicate that algorithm is for numbers of special forms; bold indicates deterministic algorithm for primality tests (current article is always in bold).